Ha a motor által kifejlesztett nyomaték megegyezik a hajtómű ellenállási nyomatékával, a hajtási sebesség állandó.
A hajtás azonban sok esetben felgyorsul vagy lelassul, pl. tranziens üzemmódban működik.
Átmeneti Az elektromos hajtásmód az egyik állandósult állapotból a másikba való átmenet üzemmódja, amikor a fordulatszám, a nyomaték és az áramerősség változik.
Az elektromos hajtások tranziens üzemmódjainak előfordulásának oka a gyártási folyamathoz kapcsolódó terhelés változása, vagy az elektromos hajtás szabályozása során gyakorolt hatás, pl. indítás, fékezés, forgásirány változtatás stb., valamint az áramellátó rendszer megszakadása.
Az elektromos hajtás mozgásegyenleténél figyelembe kell venni az összes tranziens üzemmódban ható momentumot.
Általában az elektromos hajtás mozgásegyenlete a következőképpen írható fel:
Pozitív sebességnél az elektromos hajtás mozgásegyenlete a következő formában van
A (2.10) egyenlet azt mutatja, hogy a motor által kifejlesztett nyomatékot egyensúlyban tartja az ellenállási nyomaték és a dinamikus nyomaték. A (2.9) és (2.10) egyenletekben feltételezzük, hogy a hajtás tehetetlenségi nyomatéka állandó, ami jelentős számú működtetőre igaz.
A (2.10) egyenlet elemzéséből világosan kiderül:
1) > , , azaz. megtörténik a hajtás gyorsulása;
2) mikor< , , т.е. имеет место замедление привода (очевидно, замедление привода может быть и при отрицательном значении момента двигателя);
3) amikor = , ; ebben az esetben a hajtás állandósult állapotban működik.
Dinamikus pillanat(a nyomatékegyenlet jobb oldala) csak tranziens üzemmódokban jelenik meg, amikor a hajtási sebesség változik. A hajtás gyorsulásakor ez a nyomaték a mozgás ellen irányul, fékezéskor pedig támogatja a mozgást.
3. A hajtás statikus stabilitásának fogalma.
A statikus stabilitás alatt általában egy rendszer azon képességét értjük, hogy kis zavarással önállóan vissza tudja állítani eredeti működési módját. A statikus stabilitás szükséges feltétele a rendszer állandósult üzemmódjának fennállásának, de egyáltalán nem határozza meg előre a rendszer azon képességét, hogy hirtelen zavarok, például rövidzárlatok esetén tovább tudjon működni.
3.1 ábra – Teljesítményváltozás szögnövekedéssel.
Szóval, pont Aés a szinuszos teljesítménykarakterisztika növekvő részének bármely más pontja statikailag stabil módusoknak felel meg, és fordítva, a karakterisztika csökkenő részének minden pontja statikailag instabil üzemmódnak felel meg. Ez magában foglalja a legegyszerűbb rendszer statikus stabilitásának következő formális jelét: a generátor szögének és teljesítményének növelése R ugyanazzal a jellel kell rendelkeznie, azaz, vagy a határig áthaladva:
Pozitív, ha< 90° (рис. 3.3). В этой области и возможны устойчивые установившиеся режимы работы системы. Критическим с точки зрения устойчивости в рассматриваемых условиях (при чисто индуктивной связи генератора с шинами приемной системы) является значение угла = 90°, когда достигается максимум характеристики мощности.
Az elektromos hajtás mechanikus része szilárd testek rendszere, amelyek mozgását a testek közötti mechanikai kapcsolatok határozzák meg. Ha az egyes elemek sebességei közötti összefüggéseket megadjuk, akkor az elektromos hajtás mozgásegyenlete differenciál alakú. A mozgásegyenletek írásának legáltalánosabb formája az általánosított koordinátákban megadott mozgásegyenletek (Lagrange-egyenletek):
Wk– a rendszer kinetikus energiájának tartaléka, általánosított koordinátákkal kifejezve q iés általánosított sebességek;
Qi– általánosított erő, amelyet a δ munkaösszeg határoz meg A i az esetleges elmozdulásra ható összes erő.
A Lagrange-egyenlet más formában is ábrázolható:
(2.20)
Itt L– Lagrange-függvény, amely a rendszer kinetikus és potenciális energiái közötti különbség:
L= Wk – W n.
Az egyenletek száma megegyezik a rendszer szabadságfokainak számával, és a változók száma határozza meg - általánosított koordináták, amelyek meghatározzák a rendszer helyzetét.
Írjuk fel a Lagrange-egyenleteket a rugalmas rendszerre (2.9. ábra).
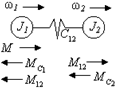
Rizs. 2.9. Kéttömegű mechanikai alkatrész tervezési diagramja.
A Lagrange függvénynek ebben az esetben a formája van
Az általánosított erő meghatározásához ki kell számítani az összes nyomaték elemi munkáját az első tömegre csökkentve egy lehetséges elmozdulásnál:
Ezért, mivel az általánosított erőt a δ elemi munkák összege határozza meg A 1 a δφ területen 1 , majd a kapott érték meghatározásához:
Hasonlóképpen a definícióhoz a következőket használjuk:
Ha a Lagrange-függvény kifejezését behelyettesítjük (2.20)-ba, a következőt kapjuk:
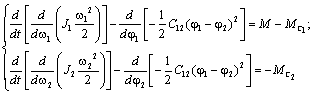
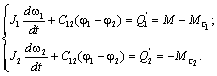
Miután kijelölte 
, kapunk:
(2.21)
Tegyük fel, hogy az első és a második tömeg közötti mechanikai kapcsolat abszolút merev, azaz. (2.10. ábra).
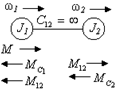
Rizs. 2.10. Kettős tömegű merev mechanikus rendszer.
Ekkor a rendszer második egyenlete a következő alakot veszi fel:
Ha behelyettesítjük a rendszer első egyenletébe, a következőt kapjuk:
(2.22)
Ezt az egyenletet néha az elektromos hajtás alapvető mozgásegyenletének is nevezik. Használatával használhatja a motor ismert elektromágneses nyomatékát M, Az ellenállási nyomaték és a teljes tehetetlenségi nyomaték felhasználásával becsülje meg az elektromos hajtás átlagos gyorsulási értékét, számítsa ki azt az időt, amely alatt a motor eléri az adott fordulatszámot, és oldjon meg egyéb problémákat, ha a rugalmas kötések hatása a mechanikai rendszerben jelentős.
Tekintsünk egy olyan mechanikai rendszert, amely nemlineáris kinematikai kapcsolatokkal rendelkezik, mint például hajtókar, billenő és más hasonló mechanizmusok (2.11. ábra). A redukciós sugár bennük a mechanizmus helyzetétől függően változó érték: .
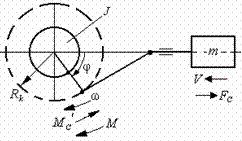
Rizs. 2.11. Mechanikai rendszer nemlineáris kinematikai kapcsolatokkal
Képzeljük el a vizsgált rendszert kéttömegű rendszerként, az első tömeg ω sebességgel forog és tehetetlenségi nyomatéka van, a második pedig lineáris sebességgel mozog Vés a teljes tömeget jelenti m elemek mereven és lineárisan kapcsolódnak a mechanizmus munkatestéhez.
Az ω és a lineáris sebességek kapcsolata V nemlineáris, és . Ahhoz, hogy egy ilyen rendszer mozgásegyenletét a rugalmas kapcsolatok figyelembevétele nélkül megkapjuk, a (2.19) Lagrange-egyenletet használjuk, a φ szöget általánosított koordinátának vesszük. Határozzuk meg az általánosított erőt:
A motorhoz lineárisan kapcsolódó tömegekre ható erők teljes ellenállási nyomatéka; a motor tengelyére hajtva;
F C– a mechanizmus munkatestére és a hozzá lineárisan kapcsolódó elemekre kifejtett összes erő eredője;
– lehetséges végtelenül kicsi tömegmozgás m.
Ezt nem nehéz belátni
Öntési sugár.
A mechanizmus statikus terhelési nyomatéka pulzáló terhelési komponenst tartalmaz, amely a φ elfordulási szög függvényében változik:
Rendszer kinetikus energia tartalék:
Itt látható a rendszer teljes tehetetlenségi nyomatéka a motor tengelyére csökkentve.
A (2.19) Lagrange-egyenlet bal oldala a következőképpen írható fel:
Így egy merev redukált láncszem mozgásegyenlete a következőképpen alakul:
(2.23)
Nemlineáris változó együtthatókkal.
Merev lineáris mechanikus kapcsolat esetén az elektromos hajtás statikus üzemmódjának egyenlete megfelel, és a következő formában van:
Ha költözéskor 
akkor vagy dinamikus tranziens folyamat megy végbe, vagy a rendszer periodikusan változó sebességű kényszermozgása.
A nemlineáris kinematikai kapcsolatokkal rendelkező mechanikai rendszerekben nincsenek statikus üzemmódok. Ha ω=const, akkor az ilyen rendszerekben állandósult állapotú dinamikus mozgási folyamat zajlik. Ennek oka, hogy a lineárisan mozgó tömegek oda-vissza mozgást végeznek, sebességük és gyorsulásuk változó mennyiségû.
Energetikai szempontból különbséget tesznek az elektromos hajtás motoros és fékezési üzemmódja között. A motor üzemmód megfelel a mechanikai energia közvetlen átviteli irányának a mechanizmus munkatestéhez. Aktív terhelésű elektromos hajtásokban, valamint elektromos hajtásban tranziens folyamatokban, amikor a mechanikai rendszer mozgása lelassul, a mechanikai energia visszakerül a mechanizmus munkatestéből a motorba.
Az elektromos hajtás mechanikus része szilárd testek rendszere, amelynek mozgása mechanikai kapcsolatok által meghatározott korlátozások alá esik. megadjuk, a mechanikában az ilyen kapcsolatokat holonomikusnak nevezzük A független változók – a rendszer helyzetét meghatározó általánosított koordináták – száma megegyezik a fokozatok számával. Ismeretes, hogy az ilyen rendszerek mozgási differenciálegyenleteinek legáltalánosabb formája az általánosított koordinátákban szereplő mozgásegyenletek (Lagrange-egyenletek).
ahol W K a rendszer kinetikus energiájának tartaléka, q i általánosított koordinátákkal és i általánosított sebességekkel kifejezve; Q i =dA i /dq i - a lehetséges dq i elmozdulásra ható összes ható erő dA 1 elemi munka összege által meghatározott általánosított erő, vagy
ahol L a Lagrange-függvény, Q" i a dA elemi munkák összege által meghatározott általános erő, az összes külső erő egy lehetséges dq i elmozdulásra. A Lagrange-függvény a kinetikus W K és a potenciális W p energiák közötti különbség rendszer, q i általánosított koordinátákkal és i általánosított sebességekkel kifejezve, azaz:
A Lagrange-egyenletek egységes és meglehetősen egyszerű módszert adnak a hajtás mechanikai részében zajló dinamikus folyamatok matematikai leírására; számukat csak a rendszer szabadságfokainak száma határozza meg.
A rendszerben a különböző szög- és lineáris mozgások egyaránt általánosított koordinátáknak tekinthetők, ezért a hajtás mechanikai részének dinamikájának a Lagrange-egyenletek segítségével történő matematikai leírásakor nincs szükség elemeinek azonos sebességre történő előzetes redukálására. A redukciós művelet végrehajtása előtt azonban a legtöbb esetben lehetetlen mennyiségileg összehasonlítani a rendszer különböző tömegeit és a köztük lévő kapcsolatok merevségét, ezért lehetetlen azonosítani a fő tömegeket és a fő rugalmas kapcsolatokat amelyek meghatározzák a tervezés során figyelembe veendő rendszer szabadságfokainak minimális számát. Ezért a fenti mechanikai tervezési diagramok összeállítása és lehetséges egyszerűsítése az összetett elektromechanikus villamos hajtásrendszerek számításának első fontos lépése, függetlenül attól, hogy milyen módszerrel nyerjük a matematikai leírásukat.
Adjuk meg az 1.2. ábrán bemutatott elektromos hajtás általánosított tervezési mechanikai áramköreinek megfelelő mozgásegyenleteket. Egy háromtömegű rugalmas rendszerben az általánosított koordináták az f 1,--f 2,--f 3 tömegek szögelmozdulásai, és megfelelnek a w 1, w 2 és w 3 általánosított sebességeknek. A Lagrange függvény alakja:
A Q" 1 általánosított erő meghatározásához ki kell számítani az első tömegre ható összes nyomaték elemi munkáját egy lehetséges elmozdulásnál
Ennélfogva,
Két másik általánosított erőt is hasonlóan definiálunk:
Az (1,34)-et behelyettesítve (1,32)-be, és figyelembe véve (1,35) és (1,36) azt kapjuk, hogy
a következő mozgásegyenletrendszer:
Az (1.37)-ben a rugalmas kötések alakváltozásaival arányos nyomatékok
a rendszer mozgó tömegei közötti rugalmas kölcsönhatás momentumai:
Az (1.38) figyelembevételével a mozgásegyenletrendszer ábrázolható formában
Az (1.39) figyelembevételével megállapíthatjuk, hogy az elektromos hajtás redukált tömegeinek mozgásegyenletei azonos típusúak. Egy fizikai törvényt (Newton második törvényét) tükröznek, amely szerint a merev test gyorsulása arányos a rá ható nyomatékok (vagy erők) összegével, beleértve azokat a nyomatékokat és erőket is, amelyeket a test más merev testeivel való rugalmas kölcsönhatás okoz. rendszer.
Nyilvánvaló, hogy nem kell újra megismételni a mozgásegyenletek levezetését, áttérve egy kéttömegű rugalmas rendszerre. Egy kéttömegű rendszer mozgását az (1.39) rendszer írja le, ahol J 3 =0 és M 23 =0
Fizikai lényegének jobb tisztázása érdekében hasznos az átmenetet a kéttömegű rugalmas rendszerről egy egyenértékű merev, redukált mechanikai láncra két lépésben. Először is tegyük fel, hogy az első és a második tömeg közötti mechanikai kapcsolat (lásd 1.2,b ábra) abszolút merev (12 =Ґ). Kéttömegű merev rendszert kapunk, melynek tervezési diagramja az 1.9. Ennek eltérése az 1.2,b ábrán látható diagramtól a w 1 =w 2 =w i tömegsebességek egyenlősége, míg az (1.40) rendszer második egyenletének megfelelően
Az (1.41) egyenlet egy merev mechanikus kapcsolat terhelését jellemzi az elektromos hajtás működése közben. Ha ezt a kifejezést behelyettesítjük az (1.40) rendszer első egyenletébe, azt kapjuk
Ezért az 1.2. ábra jelölését figyelembe véve М С = М С1 + М с2 ; J S =J 1 +J 2 Az elektromos hajtás mozgásegyenletének alakja
Ezt az egyenletet néha az elektromos hajtás alapvető mozgásegyenletének is nevezik. Valójában rendkívül nagy a jelentősége az elektromos hajtás fizikai folyamatainak elemzésében. Amint az alább látható, helyesen írja le az elektromos hajtás mechanikus részének átlagos mozgását. Ezért segítségével a motor ismert elektromágneses nyomatéka és M c és J S értékei alapján meg lehet becsülni az elektromos hajtás gyorsulásának átlagos értékét, megjósolni azt az időt, amely alatt a motor elér egy adott sebességet, és sok más gyakorlati kérdést megold, még olyan esetekben is, amikor a rugalmas kapcsolatok befolyása jelentős a rendszerben.
Mint már említettük, számos elektromos hajtás hajtóművei nemlineáris kinematikai kapcsolatokat tartalmaznak, mint például a hajtókar, a billenő és más hasonló mechanizmusok. Az ilyen mechanizmusoknál a redukciós sugár a mechanizmus helyzetétől függően változó érték, és a matematikai leírás megszerzésekor ezt a körülményt figyelembe kell venni. Különösen az 1.10. ábrán látható forgattyús mechanizmus diagramjához
ahol R k a hajtókar sugara.
Az 1.10. ábrán láthatóakhoz hasonló mechanizmusokat szem előtt tartva tekintsünk egy kéttömegű rendszert, amelynek első tömege w motorfordulatszámon forog, és az összes mereven és lineárisan összekapcsolt J 1 forgóelem teljes tehetetlenségi nyomatékát jelenti. a motor tengelye, a második tömeg pedig v lineáris sebességgel mozog, és a mechanizmus munkatestéhez mereven és lineárisan kapcsolódó elemek m össztömegét jelenti. A w és v sebességek közötti összefüggés nemlineáris, r--=--r(f). Ahhoz, hogy egy ilyen rendszer mozgásegyenletét a rugalmas kapcsolatok figyelembevétele nélkül megkapjuk, az (1.31) Lagrange-egyenletet használjuk, a φ szöget véve általánosított koordinátának. Először meghatározzuk az általánosított erőt:
ahol M c " a motorhoz lineárisan kapcsolódó tömegre ható erők teljes ellenállási nyomatéka, a motor tengelyére redukálva; F c a mechanizmus és a vele lineárisan kapcsolódó elemek munkatestére ható összes erő eredője dS a t tömeg lehetséges végtelenül kicsi mozgása.
ahol r(f)=dS/df – redukciós sugár
A vizsgált típusú nemlineáris mechanikai kapcsolat jelenlétében a mechanizmus statikus terhelési nyomatéka pulzáló terhelési komponenst tartalmaz, amely az f elfordulási szög függvényében változik:
A rendszer kinetikus energia tartaléka
itt J S (f)=J 1 +mr 2 (f) a rendszer teljes tehetetlenségi nyomatéka a motor tengelyére redukálva.
Ha erre az esetre alkalmazzuk, az (1.31) egyenlet bal oldalát a következőképpen írjuk:
Így a vizsgált esetben a merev redukált láncszem mozgásegyenlete a következő alakkal rendelkezik
Az (1.45) figyelembevételével könnyen megállapítható, hogy nemlineáris mechanikai kapcsolatok jelenlétében az elektromos hajtás mozgásegyenlete lényegesen bonyolultabbá válik, mivel nemlineárissá válik, változó együtthatókat tartalmaz a motor forgórészének szögelmozdulásától függően, és a terhelési nyomaték, amely a forgásszög periodikus függvénye. Összehasonlítva ezt az egyenletet a mozgás alapegyenletével (1.42), megbizonyosodhat arról, hogy egy elektromos hajtás alap mozgásegyenletének alkalmazása csak akkor megengedett, ha a tehetetlenségi nyomaték állandó J S =const.
Azokban az esetekben, amikor az elektromos hajtás működése során a tehetetlenségi nyomaték a saját mozgásától függetlenül megváltozik, az elektromos hajtás mozgásegyenlete kissé eltérő formát ölt olyan gépek működése során, amelyekben a munkatest térbeli pályák mentén történő mozgását az egyes mozgáskoordinátákhoz biztosított több egyedi elektromos hajtás (kotrógépek, daruk, robotok stb.) végzi. Például a robotot forgató elektromos hajtás tehetetlenségi nyomatéka a megfogó forgástengelyhez viszonyított hatótávolságától függ. A megfogó hatótávolságában bekövetkező változások nem függnek az elektromos lengőhajtás működésétől, hanem az elektromos hajtás mozgása határozza meg a hatótávolságot. Ilyen esetekben az elektromos esztergahajtás csökkentett tehetetlenségi nyomatékát a J S (t) idő független függvényének kell tekinteni. Ennek megfelelően az (1.31) egyenlet bal oldala a következőképpen lesz felírva:
és az elektromos hajtás mozgásegyenlete a következő lesz:
A J S (t) és M c (t) függvényeket az elektromos hajtás mozgásának elemzésével kell meghatározni, ami a vizsgált példában a tehetetlenségi nyomaték és a terhelés változását okozza, ez a váltó mechanizmus elektromos hajtása a megfogó hatósugara.
A kapott matematikai leírások a villamos hajtás mechanikai részében zajló dinamikus folyamatokról, általánosított diagramokkal ábrázolva, lehetővé teszik az elektromos hajtás lehetséges mozgásmódjainak elemzését. Az (1.42) által leírt rendszerben a dinamikus folyamat feltétele dw/dt№0, azaz. az elektromos hajtás sebességében bekövetkező változások jelenléte. Az elektromos hajtás statikus üzemmódjainak elemzéséhez a dw/dt=0 értéket kell beállítani. Ennek megfelelően a merev és lineáris mechanikus csatlakozásokkal rendelkező elektromos hajtás statikus üzemmódjának egyenlete a következőképpen alakul:
Ha a МНМ с mozgása során dw/dt№0, akkor vagy dinamikus tranziens folyamat, vagy állandósult állapotú dinamikus folyamat megy végbe. Ez utóbbi annak az esetnek felel meg, amikor a rendszerre alkalmazott momentumok tartalmaznak egy periodikus komponenst, amely az átmeneti folyamat után periodikusan változó sebességgel határozza meg a rendszer kényszermozgását.
A nemlineáris kinematikai kapcsolatokkal rendelkező mechanikai rendszerekben (1.10. ábra), az (1.45) pontnak megfelelően, nincsenek statikus üzemmódok. Ha dw/dt=0 és w=const, akkor az ilyen rendszerekben állandósult állapotú dinamikus mozgási folyamat zajlik. Ennek az az oka, hogy a lineárisan mozgó tömegek kényszerű oda-vissza mozgáson mennek keresztül, sebességük és gyorsulásuk változó mennyiség.
Energetikai szempontból az elektromos hajtás működési módjait motorra és fékezésre osztják, amelyek a hajtás mechanikus átvitelein keresztüli energiaáramlás irányában különböznek (lásd 1.2 §). A motor üzemmód a motor által generált mechanikai energia közvetlen átviteli irányának felel meg a mechanizmus munkatestéhez. Ez az üzemmód általában a fő a mechanikus berendezések, különösen a sebességváltók tervezésénél. Az elektromos hajtás működése során azonban gyakran felmerülnek a mechanikai energia fordított átvitelének feltételei a mechanizmus működő részéből a motorba, amelynek fékezési üzemmódban kell működnie. Különösen az aktív terhelésű elektromos hajtások esetében a motor- és fékezési módok majdnem egyformán valószínűek. Az elektromos hajtás fékezési üzemmódjai a rendszer lassításának átmeneti folyamataiban is felmerülnek, amelyek során a felszabaduló mozgási energia a megfelelő tömegekből a motorba áramolhat.
A megfogalmazott rendelkezések lehetővé teszik a motor nyomatékának előjeleire vonatkozó szabály megfogalmazását, amelyet a kapott mozgásegyenletek alkalmazásakor szem előtt kell tartani. A mechanikus erőátvitel előremenő irányában P = Mw előjele pozitív, ezért a motor menetnyomatékainak olyan előjellel kell rendelkezniük, amely megegyezik a sebesség előjelével. Fékező üzemmódban P<О, поэтому тормозные моменты двигателя должны иметь знак, противоположный знаку скорости.
A mozgásegyenletek megírásakor figyelembe vettük az általánosított tervezési diagramokon, különösen az 1.2. c. ábrán látható nyomatékok irányait. Ezért a statikus terhelési nyomatékok előjeleinek szabálya eltérő: a fékező terhelési nyomatékoknak a sebesség előjelével egybeeső előjelnek, az aktív tehermozgatásnak pedig a sebesség előjelével ellentétes előjelnek kell lennie.
Ha egy mechanikai rendszer minden elemének minden mozgásában egyenlő vagy arányos sebessége van (forgás vagy lineáris), akkor egy olyan mechanikus rendszer merevnek tekinthető, amely merev mechanikai láncszemre redukálható teljes csökkentett B tehetetlenségi nyomatékkal, pl. egytömegű rendszerben a következő nyomatékok hatnak egy forgó testre, például egy villanymotor forgórészére:
- ? M - elektromos motor által létrehozott elektromágneses nyomaték;
- ? Kisasszony - a mozgással szembeni ellenállás pillanata aktív, a gép RO-jára vonatkoztatva. Ezt a pillanatot a gravitációs erők (például emelőcsörlők, liftek stb. elektromos hajtásaiban), szélerők (például forgó toronydaruk elektromos hajtása), sűrített levegő nyomás (kompresszorok elektromos hajtása) stb. A mozgással szembeni aktív ellenállás pillanatai vagy akadályozhatják a mozgást, és mozgást hozhatnak létre;
- ? Kisasszony- a gép RO-jára alkalmazott mozgási ellenállás reaktív nyomatékai. Ezek a nyomatékok az RO mozgására adott reakcióként keletkeznek, és mindig akadályozzák a mozgást (például a fémvágó gépek fő mozgásának hajtásaiban fellépő forgácsoló erők, az elektromos ventilátorhajtások aerodinamikai erőinek nyomatéka stb.). ), co = O M g _ = 0. Reaktív pillanatok közé tartozik
с.р nyomaték a csapágyakban és a munkagép kinematikai láncának egyéb elemeiben fellépő súrlódási erőkből. A súrlódási nyomaték mindig akadályozza a mozgást a reaktív ellenállási nyomatéktól M tr nullával egyenlő sebességnél is jelen van. Ráadásul, M nyugalomban általában jelentősen meghaladja a mozgás közbeni súrlódási nyomatékot.
A mozgással szembeni ellenállás teljes momentuma s (más néven statikus pillanat) egyenlő az aktív és reaktív ellenállási momentumok összegével:
Minden mozzanat előjelét a forgási sebesség előjele határozza meg: ha a pillanat elősegíti a mozgást, akkor pozitív, ha akadályozza, akkor negatív. A p előjele mindig negatív, a ca előjele lehet negatív, ha az aktív momentum akadályozza a mozgást (például teheremelés), vagy pozitív, ha a nyomaték mozgást segít elő (például teher leengedése). Az összes nyomaték algebrai összege határozza meg az eredő ellenállási momentumot M, a motor tengelyére alkalmazva.
Tekintsük annak a villanymotornak a mozgását, amelynek a tengelyére alkalmazzuk: az elektromágneses nyomatékot, amelyet a villanymotor fejleszt M,és a mozgással szembeni ellenállás pillanata c. Newton második törvényének (2.3) megfelelően:
ahol M din a dinamikus momentum; - teljes tehetetlenségi nyomaték.
A (2.5) egyenletet nevezzük az elektromos hajtás mozgásegyenlete. Vegye figyelembe, hogy ebben az egyenletben minden nyomaték a motor tengelyére vonatkozik, és a tehetetlenségi nyomaték tükrözi az elektromos motor tengelyéhez kapcsolódó és azzal mechanikai mozgást végző összes tömeg tehetetlenségét.
Transzlációs mozgás esetén az elektromos hajtás mozgásegyenlete ennek megfelelően a következőképpen alakul:
Ahol F- a motor által kifejtett erő; F- ellenállási erő a motor rúdján a mozgással szemben; T- a motorrúdhoz kapcsolódó mozgó elemek tömegei; v a motorrúd lineáris sebessége.
Pillanat M, a motor által kifejlesztett sebességétől függ. A motor által kifejlesztett nyomaték és a fordulatszám = (co) kapcsolata határozza meg az elektromos hajtás (elektromos motor) mechanikai jellemzőit.
A mechanikai jellemzők típusát meghatározó fő paraméter az merevség(2.4. ábra)
ahol D a nyomatéknövekmény; Dso - sebességnövekedés.
A P merevség jellemzi a motor azon képességét, hogy érzékeli a tengelyére ható terhelést - c nyomatékot. Mivel a fordulatszám általában csökken a terhelési nyomaték növekedésével, a P merevség negatív érték. Ha D terhelés alkalmazásakor a DSO fordulatszám enyhén csökken, akkor a mechanikai jellemzőt veszik figyelembe kemény. Ha az alkalmazott ellenállási nyomaték azonos értékénél a sebesség jelentősen megváltozik, akkor egy ilyen jellemzőt nevezünk puha.
Az elektromos hajtás (motor) mechanikai jellemzőinek P merevsége az elektromos hajtás statikus és dinamikus jellemzőit jellemző fontos érték. Ha a mechanikai karakterisztika lineáris - 1 az ábrán. 2.4, akkor a merevsége állandó, megegyezik a karakterisztika ordinátatengelyhez viszonyított hajlásszögének érintőjével. Ha a mechanikai jellemző görbe vonalú - 2 az ábrán. 2.4, akkor a karakterisztika minden pontjában a merevség változó, és a karakterisztika adott pontjához fűződő érintő dőlésszögének érintője határozza meg.
Rizs. 2.4.
1 - egyenes; 2 - ívelt
Rizs. 2.5.
ábrán. A 2.5. ábra az elektromos motorok fő típusainak természetes mechanikai jellemzőit mutatja: 1 - független gerjesztésű egyenáramú motor, mechanikai karakterisztikája lineáris, állandó nagy merevséggel rendelkezik; 2 - soros gerjesztésű egyenáramú motor, a karakterisztikája görbe vonalú, merevsége alacsony terhelésnél, és a nyomaték növekedésével nő; 3 - aszinkron motor, a mechanikai jellemzőnek két része van - egy nagy állandó negatív merevségű munkarész és egy változó pozitív merevségű ívelt rész; 4 - a szinkronmotornak abszolút merev mechanikai jellemzője van, amelyben a sebesség nem függ a terheléstől.
ábrán látható. 2.5 motorok mechanikai jellemzőit ún természetes, mivel megfelelnek a tipikus motorkapcsoló áramkörnek, a táp névleges feszültségének és frekvenciájának, valamint a motortekercselési áramkörökben a járulékos ellenállás hiányának.
Mesterséges(vagy beállítási) mechanikai jellemzők akkor érhetők el, ha a motor indításához vagy fordulatszámának szabályozásához a tápfeszültség paramétereit megváltoztatják, vagy további elemeket vezetnek be a motor tekercseinek áramkörébe.
Rizs. 2.V. A mozgással szembeni ellenállás pillanatainak a sebességtől való függése egyes munkagépeknél
A gép RO-ján létrejövő c mozgással szembeni ellenállás pillanata is függhet a sebességtől. Ez a függőség az a munkagép mechanikai jellemzői (makhantma) c = (co) - egyedi a különböző típusú technológiai gépekhez. ábrán. A 2.6. ábra a fő munkagéptípusokra jellemző jellemzőket mutatja: 1 - vágó munkaelemmel rendelkező gépek, ha a vágóelemmel eltávolított réteg vastagsága állandó, akkor az ellenállási nyomaték nem függ a sebességtől; 2 - olyan gépek, amelyeknél az ellenállási nyomatékot főként súrlódási erők határozzák meg (például szállítószalagok), az ellenállási nyomaték állandó, de indításkor a statikus súrlódási erők meghaladhatják a mozgás közbeni súrlódási erőket; 3 - emelőszerkezetek, a statikus nyomaték a természetben aktív, és nem függ a sebességtől, ennek a jellemzőnek az a jellemzője, hogy a teher felemelésének pillanata valamivel magasabb, mint a teher leeresztésének ellenállási pillanata, ami a teher felvételének köszönhető. figyelembe venni a fogaskerekek mechanikai veszteségeit; 4 - turbó mechanizmusok (centrifugális és axiális ventilátorok és szivattyúk), ezeknek a gépeknek az ellenállási nyomatéka jelentősen függ a fordulatszámtól, a ventilátoroknál arányos a fordulatszám négyzetével M s = ko); 5 - tekercselő berendezések és egyéb gépek, amelyekhez technológiailag szükséges az állandó teljesítményű működés.
Meg kell jegyezni, hogy a munkagép tengelyén a mechanikai jellemzői által meghatározott nyomatékok nem veszik figyelembe a nyomaték dinamikus összetevőjét, amely a fordulatszám megváltozásakor következik be.
Ha a motor által kifejlesztett nyomaték egyenlő a mozgással szembeni ellenállás pillanatával, akkor a (2.5)-ből az következik, hogy M = M s, M tsh =És
azok. egy merev mechanikus rendszer állandó sebességgel fog működni. Ez a működési mód az alapított. A mozgással szembeni ellenállás pillanatát ún statikus pillanat, hiszen az elektromos hajtás állandósult működési állapotát jellemzi.
Rizs. 2.7.
Grafikusan az állandósult üzemi állapotot (2.8) a motor mechanikai jellemzőinek metszéspontja o) = () határozza meg a mechanizmus mechanikai jellemzőivel.
c = (co) (2.7. ábra). Ennek a feltételnek a teljesítése az állandósult állapothoz kötelező, de ellenőrizni kell ennek az üzemmódnak a stabilitását.
Tekintsük egy aszinkron motor mechanikai jellemzőit (lásd 2.7. ábra). A mozgással szembeni ellenállás pillanata – statikus pillanat Kisasszony nem függ a fordulatszámtól - ennek a karakterisztikának a merevsége (З с = . A motor és a statikus nyomaték karakterisztikája két ponton metszi egymást AÉs BAN BEN. Ha egy ponton dolgozva A a fordulatszám bármilyen okból növekszik, kisebb lesz c, dyne A. Ha az A pontban végzett munka sebessége csökken, akkor a motor nyomatéka nagyobb lesz, és a fordulatszám visszatér a ponthoz A.Állandó állapotú működés egy ponton A fenntartható lesz.
Amikor egy ponton dolgozik BAN BEN a kép az ellenkezője. Ha a fordulatszám felfelé változik, akkor a motor nyomatéka nagyobb lesz, és a gyorsulás folytatódik. Ha a fordulatszám csökkenés irányába tér el, a motor nyomatéka kisebb lesz, mint c, és a motor leáll. Állandó állapot egy ponton BAN BEN instabil. Az állandósult állapot stabilitási feltétele úgy fogalmazható meg, hogy p És ez a feltétel a ponton teljesül BAN BEN nem hajtják végre.
Elektromos hajtás mozgásának alapegyenlete.
Elektromechanikus rendszer esetén a teljesítményegyensúly feltételnek bármikor teljesülnie kell:
Ahol 
- a motor által a tengelyre szállított teljesítmény;
- statikus ellenállási erők ereje;
- dinamikus erő, a mozgási energia megváltoztatására megy 
olyan folyamatokban, ahol a motor fordulatszáma változik.
A kinetikus energia egyenlete viszont fel lesz írva:
Vagy a dinamikus teljesítményhez:
Ha 
És 
idővel változik, a következőket kapjuk:
A teljesítményértékek egyenlővé tételével kapjuk:
Ez a függőség az elektromos hajtás mozgásegyenlete. A legtöbb mechanizmushoz 
. Ekkor az egyenlet a következő alakot veszi fel:
Elemezzük ezt az egyenletet:
Az elektromos hajtás mozgásának alapegyenlete minden mérnöki számítás alapja. Ennek alapján számításokat végeznek, például egy motordiagramot, kiválasztanak egy motort, kiszámítják az indítási nyomatékokat és áramokat, valamint értékelik az elektromos hajtás dinamikáját.
Alapfogalmak az elektromos hajtás stabilitásával kapcsolatban.
Az elektromos hajtás stabilitását a motor mechanikai jellemzőinek és a hajtómű mechanikai jellemzőinek összehasonlításával határozzuk meg ( 
És 
). Nézzük a vérnyomás példáját.
Tekintsük az aktuátorok három mechanikai jellemzőjét:
Ebben az üzemmódban a motor legyőzi a terhelési nyomatékot és a mechanikai veszteséggel járó nyomatékot. A működési mód stabil.
Ebben a módban két metszéspontunk van (2 és 3). A sebesség fenntartható 
. Mivel a fordulatszám kis eltérését ellentétes előjelű (wMiliwM) nyomatékváltozás kompenzálja.
A 3. ponthoz wM.
Az elektromos hajtás indítási és lassítási idejének meghatározása
Az indítási idő az elektromos hajtás mozgásának alapegyenlete alapján határozható meg:
.
Különítsük el az időkomponenst ebből az egyenletből:
;
Ezt a kifejezést integrálva a következőket kapjuk:
.
Ez az egyenlet határozza meg a sebesség emelkedési idejét 0-ról a végső (állandó) sebességre.
A fékezési idő a következő képlettel számítható ki:
Az elektromos hajtás termikus üzemmódjai. Az elektromos motor teljesítményének kiszámításának és kiválasztásának jellemzői különféle hőviszonyok között.
Az elektromos gép működési módja a váltakozó periódusok kialakult rendje, amelyet a terhelés nagysága és időtartama, a leállások, a fékezések, az indítások és a hátramenetek jellemeznek az üzemeltetés során.
1. Hosszú módS1
– állandó névleges terhelés mellett 
a motor olyan sokáig működik, hogy minden alkatrészének túlmelegedési hőmérséklete eléri az állandósult értéket 
. Vannak folyamatos üzemmódok állandó terhelés(1. ábra) és azzal változó terhelés(2. ábra).
2. Rövid távú üzemmódS2
– amikor az állandó névleges terhelés időszakai váltakoznak a motor leállási időszakaival (3. ábra). Ebben az esetben a motor működési időszakai 
olyan rövid, hogy a motor minden részének fűtési hőmérséklete nem éri el az állandósult értéket, és a motor leállási időszakai olyan hosszúak, hogy a motor minden részének van ideje lehűlni környezeti hőmérsékletre. A szabvány a töltési periódusok időtartamát 10, 30, 60 és 90 percben határozza meg. A rövid távú üzemmód szimbóluma a töltési időszak időtartamát jelzi, például S2 - 30 perc.
3. S3 szakaszos üzemmód – amikor a motor rövid ideig üzemel 
váltakoznak a motor leállási időszakaival 
és a munkavégzés ideje alatt 
a hőmérséklet-emelkedésnek nincs ideje az állandósult állapot elérésére, és a szünet alatt a motor egyes részeinek nincs ideje lehűlni a környezeti hőmérsékletre. A szakaszos üzemmódban a teljes működési idő időszakosan ismétlődő ciklusokra van felosztva 
.
Szakaszos üzemben a motorfűtés grafikonja úgy néz ki, mint egy fűrészfog-görbe (4. ábra). Amikor a motor eléri a túlmelegedési hőmérséklet állandó értékét, amely megfelel a szakaszos üzemmódnak 
, a motor túlmelegedési hőmérséklete továbbra is ingadozik 
előtt 
. Ahol 
alacsonyabb, mint a megállapított túlmelegedési hőmérséklet, amely akkor fordulna elő, ha a motor hosszabb ideig üzemel ( 
<
).
A szakaszos üzemmódra jellemző relatív hosszabefogadási élettartam: 
.
A jelenlegi szabvány névleges szakaszos üzemmódokat ír elő 15, 25, 40 és 60%-os munkaciklussal (hosszú távú üzemmód esetén 100 %).
A szakaszos üzemmód szimbólumában a munkaciklus értéke látható, például S3-40%.
Olyan motor kiválasztásakor, amelynek útlevelében a teljesítmény PV = 100%, az újraszámítást a következő képlet segítségével kell elvégezni:
.
A figyelembe vett három névleges mód alapvetőnek tekinthető. A szabvány további módokat is biztosít:
S4 szakaszos üzemmód gyakori indítással, óránkénti indítások számával 30, 60, 120 vagy 240;
szakaszos S5 üzemmód gyakori indításokkal és elektromos fékezéssel minden ciklus végén;
S6 mozgó üzemmód gyakori hátramenettel és elektromos fékezéssel;
S7 mozgó üzemmód gyakori indítással, hátramenettel és elektromos fékezéssel;
S8 mozgó üzemmód két vagy több különböző sebességgel;
1. ábra 2. ábra
3. ábra 4. ábra
| " |
